干货 纯电动汽车动力电池包结构静力分析及优化设计

  动力电池包作为纯电动汽车的唯一动力源，承受着电池组等模块的质量，因此其强度、刚度一定要满足使用上的要求才能够保证行驶的安全性。在建立其有限元模型的基础上，分析了电池包结构在弯曲工况、紧急制动工况、高速转弯工况、垂直极限工况以及扭转工况下的强度、刚度。分析结果为，在垂直极限工况下，电池包底板的受力情况最为恶劣，因此对原有模型做出了改进，改变底板加强筋的布置形式。经过相同工况的模拟，发现在力学性能提升的基础上，整体质量得以减轻，实现了轻量化的目标。

  小型纯电动汽车作为我们国家新能源汽车产业化的战略车型之一，得到了人们慢慢的变多的关注。动力电池包作为纯电动汽车的唯一动力源，起着保证电池组正常、安全工作的关键作用。本文对国内某一微型纯电动汽车的电池包的结构可以进行静力分析，计算出不同行驶工况中结构受到外部载荷时的应力与应变情况，并对结构的强度、刚度进行校核，发现原有结构中存在不足的地方，对其进行了相应地优化设计，使得电池包结构在使用性能提高的同时，自身的重量降低。

  本文所研究的电池包是一种箱体结构，如图1所示，由高强度钢板焊接而成。因此采用板壳单元模拟电池包结构。为减少模型前处理工作量，并不影响总体计算精度的前提下，在建立电池包有限元模型时，做出了以下的简化工作：如忽略一些尺寸较小的倒角、圆角、工艺孔等结构。

  边界条件约束是结构有限元分析中的一个重要部分。约束的正确性决定着计算分析结果的准确性。由于电池包通过7个螺栓与车身连接，因此对连接的部分施加固定约束。

  电池箱底板需承受较大的载荷，因此选用DC01型号的高强度冷轧钢板。材料参数见表1。

  由于此款电池包应用于微型纯电动汽车，其主要在城市路面上行驶，因此对其在行驶过程中可能遇到的五种工况做多元化的分析。即弯曲、制动、转弯、垂直极限和扭转五种工况。

  电池包满载静止工况主要是用来模拟电动汽车静止或者在路况较好的路面上行驶时的结构应力分布及变形情况。在这种工况下，电池包主要受到的载荷是包括电池包中的电池模块、控制模块以及连接部件等质量在重力加速度作用下所产生的重力。

  由于电池包结构通过七个螺栓与车身相连接，所以电池包结构只需要承载电池包自身的重力即可而无需考虑到整车上的乘员以及货物的质量。该电池包的整备质量为140kg，取重力加速度g=9.8N/m2。因此要对结构施加的载荷为F=mg=140*9.8=1372N。在有限元模型中，将载荷施加在结构的重心上。

  经过ANSYS软件分析计算之后，得到了电池包结构的应力与应变云图，如图1.1。

  从图中的数据能够准确的看出，结构中应力最大处的应力为85.775MPa,出现在吊耳和底部支撑加强筋的边缘，这主要是因为电池包尺寸较大，加强筋的跨度比较大加之处在电池包的两端，因此应力会比较集中。但是最大应力85.775MPa仍远小于材料的屈服极限, 因此结构是安全的。

  从应变云图中，能够准确的看出最大变形量为0.78823mm,出现在承重底板的中心处。这样的变形量虽然不是很大，不影响结构的使用功能，但是还有较大的优化空间。

  电池包高速制动工况将模拟车辆在行驶过程中紧急制动时的载荷情况。车辆在制动时，电池包除了承受自身的重力外，还将受到纵向制动加速度引起的惯性力作用。而惯性力的大小则主要根据制动加速度的大小以及电池包的重量这两个参数。

  车辆的最大制动加速度可近似由如下关系式求得，即a=v2/2s，v为车辆的行驶速度，s为将制动踏板处于最大行程所得制动距离。测得最大制动加速度为0.8g=7.84m/s2。对电池包的重心施加载荷，载荷分为两部分，其一是电池包本身的重力F1=mg=140*9.8=1372N，其二则是作用在电池包上的惯性力F2=ma=140*0.8*9.8=1097.6N。

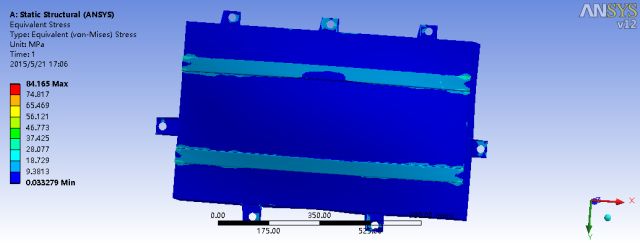
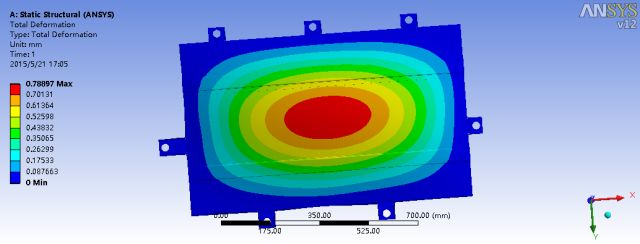
  从图中能够准确的看出电池包的最大应变值为0.78897mm，最大变形的位置仍然在底板的中心位置，最大应力值为84.165MPa,大多分布在与底部支撑加强筋的边缘与x方向的两个吊耳上。为了得出吊耳具体的受力应变应力情况，我们将对吊耳进行局部的有限元分析，对其进行单独的模型建立，并且划分网格，将吊耳所受到的载荷独立地施加在吊耳上，以此来分析吊耳的受力情况。对吊耳的上侧方形凸台面上受力的圆环面施加-Z方向，大小为F=20*9.8=196N的力，同时在受制动惯性力的圆柱面上施加-X方向，大小为156.8N的力。

  由于吊耳通过点焊方式与电池包整体的结构连接，所以对8个焊点连接处设置固定约束。

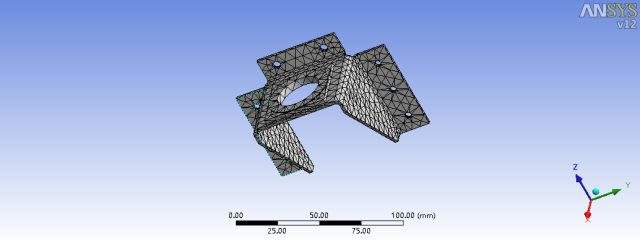
  由应力云图能够准确的看出，吊耳最大应力为23.036MPa,应力比较集中的地方在吊耳下方的焊点处和上方方形凸台的外侧边缘，因为外缘的材料较少所以应力会比较集中，但还是远远小于材料的屈服极限的，因此结构是安全的。

  车辆在高速转弯时，车身因离心力作用而产生侧向载荷，由于动力电池包是与车身连接在一起的，所以在车辆高速转弯时，电池包也将承受一定的侧向载荷。离心加速度的大小由转弯半径与行驶车速的高低决定。在此工况下电池包需要承受的是自身的重力与离心力载荷。

  对于高速转弯工况，在电池包上附加0.5g的侧向加速度来模拟转弯工况下电池包结构所受的载荷。所以要施加的载荷为两部分，其一是电池包的自重F1=140*9.8=1372N，其二是指向一侧的离心力，不妨取离心力方向是向左的，即F2=140*0.5*9.8=686N。

  由上图能够准确的看出，应变较大的地方在支承电池组的地板中心处，应变最大值为0.79192mm。因此在之后的结构改进工作中要对此进行优化。

  由于离心力载荷施加的是向左，所以位于电池包左右两侧的吊耳所受的拉压应力会略偏大。但是其最大应力值的为85.768Mpa,还是小于材料的屈服极限的。

  垂直极限工况是指车辆行驶在凹凸不平路面上时，发生垂直方向的颠簸由此产生垂直方向的载荷，引起结构发生变形的工况[1]。

  在此工况下会发生的极限情况，就是车辆垂直方向载荷的变化，依据相关文献[2]，此工况下能够达到的最大垂向加速度为1g，再加上电池包本身的重力加速度，因此要施加的载荷力F=2mg=2*140*9.8=2744N。

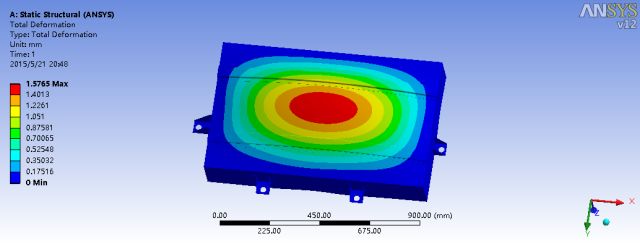
  由上图能够准确的看出，在2g垂向载荷作用下电池包底部的变形是相当明显的，最大应变值达到了1.5765mm，最大应力值达到了171.55MPa。因此加强支承底板中心处的强度是非常必要的。

  当电动汽车行驶在凹凸不平的路面上时，会发生某个车轮被抬高而另一个车轮悬空的情况。此时，由于车辆的左右两侧受力不对称，电池包会产生就比较剧烈的扭转，如果结构不能确保足够大的扭转刚度，那么电池包结构就会发生严重的变形，因此导致电池包内部的电池受到挤压，最终会发生电池组错位、电池溶液泄露、短路等危险现象[3]。

  当电池包的两侧受到不对称的载荷时，就会由于有扭矩的作用而使得电池包产生扭转变形，在此工况下，设置两边的受力差值为1500N，即在电池包的一侧施加大小为1500N的力，另一侧做固定，对有两个吊耳的一侧施加固定约束，有三个吊耳的一侧的限制X、Y方向的自由度，最后分析受力一侧的挠度，从而能够求得电池包的扭转刚度。

  由图中能够准确的看出，扭转工况下的最大应变出现在受力一侧最大应变值为0.36355mm，在1500N的集中力作用下，这样的变形量还不足以使得电池发生错位，因此，电池包结构有充足的扭转刚度。而此时最大应力值为190.95MPa，大多分布在于电池包的宽为93mm的吊耳上。

  1.针对上述第一个问题，根本原因是电池包的横向尺寸比较大，达到1000mm，因此底部支承板加强筋的跨度比较大，加之其中部所受载荷比较大，导致中部变形量也较大，所以其边缘处的受力情况相对来说比较复杂，因此应力会比较集中。所以考虑将底部支承板加强筋改成与原来垂直的方向，并从原来的2条加强筋增加到3条。

  2.针对第二个问题，还在于加强筋之间的间距较大，对底板中部的支撑作用较小，所以在上述基础上，将一根加强筋的位置放在底板的中心部位，这样就可以轻松又有效地增加对底板的支承，从而减小底板的变形量。

  对电池包的结构可以进行改造，其三维模型如下图所示，中间的加强筋经过电池包的中心点，两侧的加强筋距离中间的加强筋为218mm。

  将新模型导入ANSYS软件，分别对其施加上文所述的5种不同工况下的载荷，分析其应力与应变情况。得出改进前后结构的最大应力、应变值的变动情况，为了更加鲜明地作对比，将结果制成如下条形图。

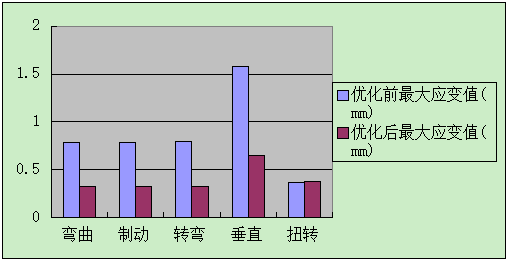
  由对比图中能清楚地看出，改进前后电池包结构的性能发生了较大的变化，在各工况下，改进后结构的应力最大值均有较大幅度的减小，应变值除了扭转工况下有很小的增加，其他工况下的减小量均达到了58%左右，可见改善的效果是相当明显的。同时，有必要注意一下的是，所使用加强筋的总长度由2000mm减少到1836mm，在截面形状不变的情况下，材料的使用减少了164mm，减轻了整个电池包的重量，在性能提高的基础上实现了轻量化。

  本文在建立了某款纯电动汽车动力电池包有限元模型的基础上，对其在不同工况下进行了静力学分析，得到了相应地的应力应变情况。在总结了不同工况下电池包存在的共同问题之后，提出了对原有模型的优化设计的具体方案，并在ANSYS中对新模型施加五种相同工况下的相应载荷来优化设计的验证，发现改进后模型的最大应力与应变值都会降低，其中最大应力值降幅达到了58.57%，并且在保证使用性能的基础上减少了材料的使用。因此，电池包结构的优化设计是成功的。

  [2] 邓丽梅. 汽车车身有限元分析与研究 [D].武汉武汉理工大学，硕士学位论文，2007